You don't need to be wealthy to succeed at portfolio investment. But for your investment portfolio's returns to match or even outperform the broader stock market, you need some foundational knowledge about how to invest. Let's go through the basics of how to build a solid investment portfolio and pick good stocks for beginner investors.

Portfolio investment defined
A portfolio investment is one you make with the expectation the holding will either gain value or generate interest or dividend income. A portfolio investment differs from an investment in a business you directly operate in that your stake is passive, meaning you don't make management decisions. Your investment portfolio can include:
- Stocks
- Bonds
- Mutual funds
- Exchange-traded funds (ETFs)
- Real estate investments, like real estate investment trusts (REITs)
- Cash equivalents, such as certificates of deposit (CDs) or savings accounts
Understanding risk tolerance and asset allocation
The first step is to decide the level of risk you're comfortable with. Higher-risk investments can generate high rewards, but they also can result in large losses. Generally, investing in stocks produces the highest returns, while investing in bonds increases the stability of your portfolio's value.
Younger people saving for retirement can invest primarily in stocks to maximize the growth of their portfolio's value because they have more time to recover if it incurs any large losses. Later in life, those same investors can concentrate their portfolios more heavily in bonds as they approach retirement and their risk tolerance decreases.
Some investors choose to further diversify their portfolios through asset allocation. Basically, this means having more than one asset class in your investment portfolio's holdings. This could include equities like stocks and funds, fixed-income investments like bonds, and cash or CDs.
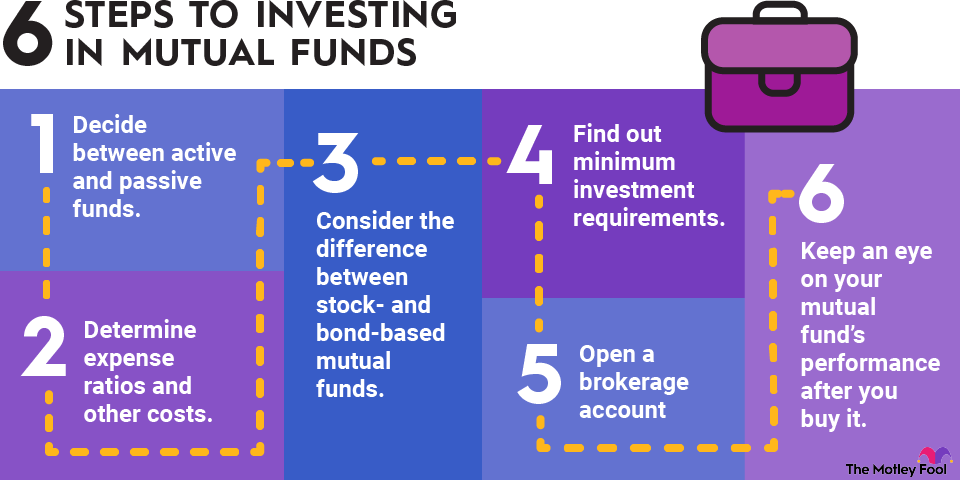
This kind of portfolio diversification is key to managing the risks of individual investments. Mutual funds and exchange-traded funds (ETFs), which provide automatic exposure to hundreds or even thousands of companies, are great options to help any beginner investor diversify their holdings.
Having a mix of types of investment accounts is also a good idea. Investing in a tax-advantaged retirement account, such as a 401(k) or an individual retirement account (IRA), is a smart choice for any investor who's eligible. You may also want to establish a taxable brokerage account, which enables you to access your money at any time without paying an early withdrawal penalty.
Diversifying the investments in your portfolio in a way that diversifies your tax exposure is also a smart strategy. Traditional 401(k)s and IRAs can accept pre-tax dollars as contributions, with taxation occurring on withdrawals in retirement. Roth 401(k)s and Roth IRAs accept after-tax dollars, which enables tax-free withdrawals in retirement. Maintaining a combination of traditional and Roth accounts can help you save on taxes both now and in retirement.
How to start your investment portfolio
Building a winning investment portfolio is easier than you think. Here's how to get started if you're just learning how to invest.
1. Look around you
One piece of advice for beginning investors is to buy stock in companies you already know and like.
Are you into fitness? You might want to research Nike (NKE -0.68%) or lululemon Athletica (LULU +1.43%).
Do you often eat at Texas Roadhouse (TXRH +3.10%) or McDonald's (MCD -0.78%)? Shares of these companies might be good picks for you.
Were you impressed with the theme park operations when you visited Disney World? Or have you seen every Pixar movie ever made? Then check out The Walt Disney Company (DIS -1.69%) stock.
You should consider investing in businesses that play a role in your own life because those are companies you already know something about. You can invest more confidently in familiar brands than in companies you've read about but don't really understand. Investing in small-cap and mid-cap companies that you're familiar with but that aren't widely known is a way to get in on great companies while they're still growth stocks.
Think about what innovative products or services are meeting your needs, or those of your family or community, and offer great customer service. Those companies could be the next Netflix (NFLX -2.95%) or Airbnb (ABNB -2.00%).
2. Do your research
It's not enough to know or even like a company; you need to have some confidence that the value of the company is increasing over time. To find out what you need to know, look at the company's financial statements.
While all publicly traded companies post their financial performance results online, what's published by the companies may be confusing for many investors. But you don't need to be a financial professional to read through a few quarterly and annual reports to ascertain whether a company is increasing its revenue, profit, and cash flow. Reading these reports can give you both a qualitative and quantitative sense of how well a company is performing.
Portfolio investment example
While there's no single approach to investing that's right for everyone, building a high-performing investment portfolio always involves:
- Clearly defining your financial goals
- Understanding your risk tolerance
- Conducting the necessary research
Let's assume one of your major investment goals is diversifying your portfolio. You decide to invest in an S&P 500 index fund, which provides instant exposure to 500 of the largest publicly traded companies in the U.S. To diversify your holdings and include companies with varying growth potential, you can also buy small-cap and mid-cap stocks. To diversify your geographic exposure, you can contribute money to an index fund that tracks non-U.S. stock markets.
Your choices for how to diversify are nearly endless. You can buy bonds, ETFs, and mutual funds. You can invest money in a 401(k) plan sponsored by your employer in addition to independently establishing an IRA. You can receive income by investing in dividend-paying stocks.
If you want to buy the stocks of specific companies, then inevitably you need to choose among competing options. Let's say you want to invest in either Walmart (NYSE:WMT) or Target (TGT +2.82%). Below are their annual financial results, based on data contained in their most recent 10-K reports for the fiscal year ending Jan. 31, 2024:
Company | Total Sales Growth | Same-Store Sales Growth | Adjusted Earnings Per Share |
|---|---|---|---|
Walmart | 5% | 4.5% | $6.65 |
Target | (3.1%) | 0.1% | $8.86 |
Looking at this data, you can evaluate two key metrics:
- Sales growth: Are both companies expanding their sales year over year? Which company is doing so faster? Same-store sales growth is a useful metric because it eliminates many variables to more clearly indicate how well a retail company is performing.
- Profitability: Are both companies profitable? Which company is more profitable on a per-share basis? Earnings per share is a useful metric to help you understand and compare the profitability of similar companies.
Related investing topics
Another metric you can consider is how much free cash each company has on hand. Companies with healthy cash balances can better cope with any financial difficulties that may arise.
Walmart increased its sales for the fiscal year, overall and per store, while Target experienced a modest drop in overall sales -- yet it still posted higher earnings per share.
Other relevant factors might explain the sales growth differences, and other salient reasons could make Walmart stock a better buy (or a better buy for you). You could decide to invest in both companies, but if doing so would create too much portfolio exposure to retail stocks, then you may want to choose one and complement it with the stock of a company operating in another stock market sector that interests you.
You shouldn't expect to receive above-market returns from every stock in your portfolio, but if you diversify your holdings and choose well, enough of your investments should succeed to result in your portfolio steadily gaining value over time.