Most bonds in the investment universe work by providing a stream of regular interest payments to the investor over the life of the bond. When a typical bond comes due -- or when the bond reaches its maturity -- the investor receives the face value of the bond, and the transaction formally ends.
Zero-coupon bonds are debt securities that are sold at deep discounts to face value. As their name indicates, they don't pay periodic interest payments, but they do reach full maturity at a certain point, and the bondholder then receives the face value of the bond, plus any accrued interest.
Understanding zero-coupon bonds
Zero-coupon bonds make money by being sold to investors at substantial discounts to face value. Zero-coupon bonds compensate for not paying any interest over the life of the bond by being available for far less than face value. Put another way, without a deep discount, zero-coupon bonds wouldn't be especially competitive.
Even though you can expect to receive the face value of a zero- coupon bond if you hold it to maturity, you need to prepare to not receive any interest until the bond comes due. In many cases, bonds won't mature for decades. The IRS, however, does require that you recognize phantom income in the form of imputed interest -- another way of saying that the IRS taxes you on the theoretical income you've earned as a zero-coupon bondholder even if you never actually received any interest payments.
Zero-coupon bonds are also subject to all of the other baseline bond risks, including interest rate risk, default risk, and inflation risks. As we'll discuss below, some of these risks are magnified in zero-coupon securities. Although buying zeros can make sense in a limited number of circumstances, you'll certainly want to understand the ways in which you could lose money along the way -- especially with most zero-coupon bond terms lasting more than a decade.
Zero-coupon bonds vs. regular bonds
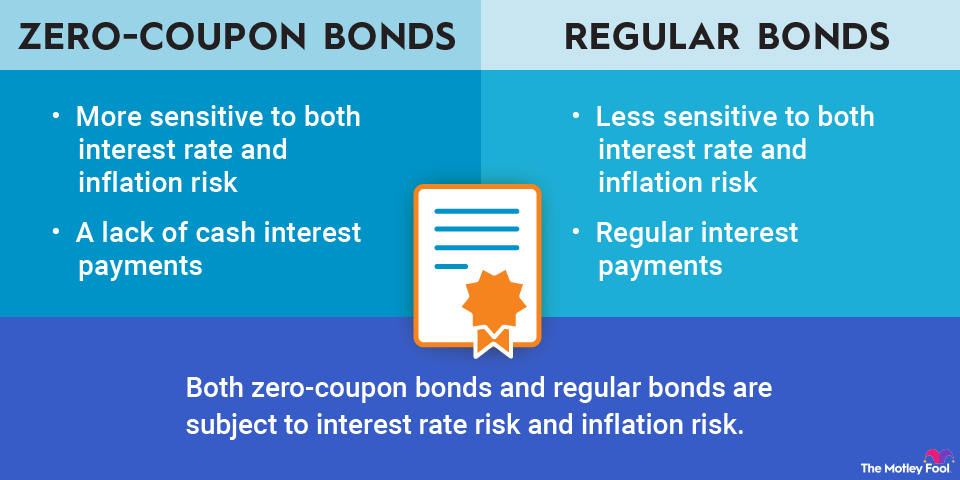
Zero-coupon bonds share some similarities with "regular" bonds. First, much like regular bonds, zeros are subject to interest rate risk. In short, we know that as interest rates rise, existing bond prices fall. With zero-coupon bonds, interest rate risk is at its highest since zeros display unusual sensitivity to changes in interest rates -- although the underlying inverse relationship to interest rates is the same as most mainstream bonds.
Zero-coupon bonds are also subject to inflation risk. Much of the bond market as a whole is subject to inflationary pressure, which is another way of saying that bonds as an asset class tend to lose their purchasing power over long periods of time. The effect is especially magnified in times of significant inflation (like in early 2022) and is also magnified in zero-coupon securities, where there are no interest payments to offset declining purchasing power.
Finally, although also similar to regular bonds, zero-coupon bonds can either be government-issued, corporate, or municipal. Depending on the issuer, zero-coupon municipal bonds may generate tax-free imputed income, which means you won't have to pay tax until the bond matures -- usually many years in the future. Corporate zeros, on the other hand, usually will lead to some annual tax liability even if you don't receive any interest in cash.
At the same time, zero-coupon bonds sport some drastic differences from regular bonds. First, zeros are especially sensitive to both interest rate and inflation risk -- even more than the majority of most regular bonds. While you'll be able to buy zeros at deep discounts to face value, you won't receive anything in return for your investment until the term of the bond ends. Along the way, you'll be subject to higher levels of interest rate risk (if interest rates rise) and inflation risk (if prices rise generally in the economy). Consequently, you may be left with a weak-performing asset if you buy and hold zeros at the wrong time.
Second, a lack of cash interest payments can make zeros even less appealing. For example, if rates rise and inflation peaks, zero-coupon bond investors don't receive any cash interest to help soften losses. This can make zeros a difficult sell for many bond investors, especially because most lean on regular interest payments as a major factor in wanting to hold bonds.
Finally, zero-coupon bonds do offer face value at maturity, but you have to be able to endure significant volatility along the way -- more than many bond investors may be willing to tolerate. This is especially true of long-dated zero-coupon bonds or those maturing many years (and even decades) into the future. Keeping this in mind, volatility can also happen to the upside, especially when interest rates fall; this can create a better-than-expected outcome for zero-coupon bondholders.
How to price a zero-coupon bond
Finding the price for a zero-coupon bond is very straightforward, in part because there are no periodic interest payments. Here are a couple of examples that illustrate how zeros are typically priced.
Example 1
For the first example (and to keep things simple), assume that imputed interest compounds annually.
Say you want to purchase a bond with a face value of $10,000, 10 years to maturity, and 5% imputed interest. To find the current price of the bond, you'd follow the formula:
Price of Zero-Coupon Bond = Face Value / (1+ interest rate) ^ time to maturity
Price of Zero-Coupon Bond = $10,000 / (1.05) ^ 10 = $6,139.11
This means that given the above variables, you'd be able to purchase a bond for $6,139.11, wait 10 years, and redeem it for $10,000. Remember that the market price of the bond will fluctuate -- possibly significantly -- over the remaining life of the bond.
Example 2
In a second example, assume that imputed interest compounds semiannually.
Price of Zero-Coupon Bond = Face Value / (1+ interest rate/2) ^ time to maturity*2
Price of Zero-Coupon Bond = $10,000 / (1.025) ^ 20 = $6,102.77
With semiannual compounding, we see the bond offered at an initially deeper discount than if imputed interest were to compound annually. Zero-coupon bonds, again, do not actually pay interest out as time passes but instead generate phantom income that is only actually paid when the bond finally matures.
Most zero-coupon bonds compound semiannually, so the second formula is more applicable for general calculation purposes.
Also, because they do not generate regular interest payments, zero-coupon bonds do not carry reinvestment rate risk -- a risk found with most other types of bonds.
Pros and cons of zero-coupon bonds
Related investing topics
Pros | Cons |
|---|---|
Can be obtained at a significant discount to face value.
Can be useful for settling obligations of known amounts at a specific date in the future.
Only a remote chance of default in federally issued zeros.
Can be sold prior to maturity if necessary. | Especially sensitive to interest rate and inflation risk.
No cash interest for the life of the bond.
Imputed "phantom" income creates additional tax liability.
Display a poor risk-return profile, generally speaking. |
The bottom line
Zero-coupon bonds do have a place in many portfolios, especially for those with an already diversified bond allocation looking for different exposure. However, as of early 2022, zeros offered a generally poor risk-return outlook because of rising interest rates and spiking inflation, which has resulted in punishing returns for zeros. With that said, there still can be a place for zeros in a diversified portfolio for the right investor -- especially if they have a long time horizon and are willing to hold to maturity.