What is net present value?
What is net present value?
Net present value (NPV) is a number investors calculate to determine the profitability of a proposed project. NPV can be very useful for analyzing an investment in a company or a new project within a company.
NPV considers all projected cash inflows and outflows and employs a concept known as the time value of money to determine whether a particular investment is likely to generate gains or losses. NPV as a metric confers a few unique advantages, and it also has some disadvantages that render it irrelevant for certain investment decisions.
How net present value works
How net present value works
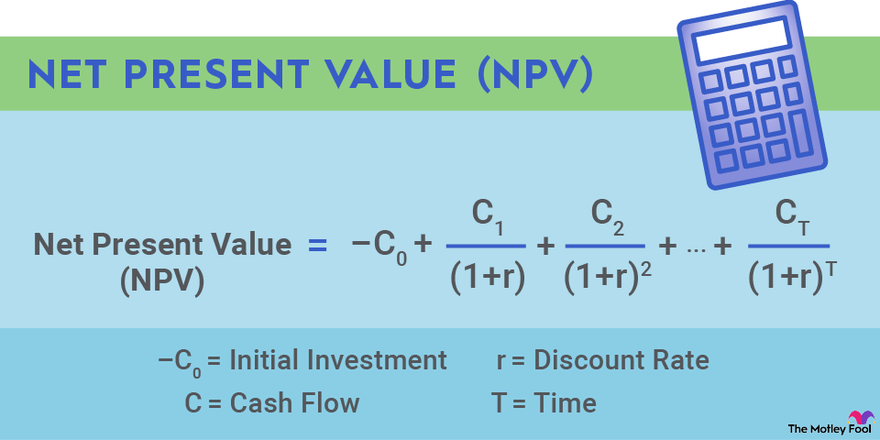
To understand NPV, first let's examine the time value of money, which is the idea that having a dollar in the future is not worth as much as having that dollar today. By discounting future cash flows based on how far in the future they are projected to occur, and then adding together each of those discounted values, a number is obtained that represents the net value at present of those projected cash flows. A positive number indicates that the project is profitable on a net basis, while a negative number indicates that the project would create a net loss.
Time Value of Money (TVM)
The initial investment required to launch the project is the first term in this equation, and it's negative since it represents an outlay of money.
The second term represents the first cash flow, perhaps for the first year, and it may be negative if the project is not profitable in the first year of operations. The third term represents the cash flow for the second year, and so on, for the number of projected years.
A discount rate, r, is applied, with (1+r) raised to the number of years in the future a cash flow is projected. The "T" exponent in the denominator of this NPV equation is core to the time value of money concept since high T values cause far-future cash flows to be exponentially more discounted.
This equation can be performed in Excel, on a financial calculator, or, for the ambitious, computed by hand.
How to calculate net present value
How to calculate net present value
Using the data below, let's walk through an example to better understand how to determine a project's NPV.
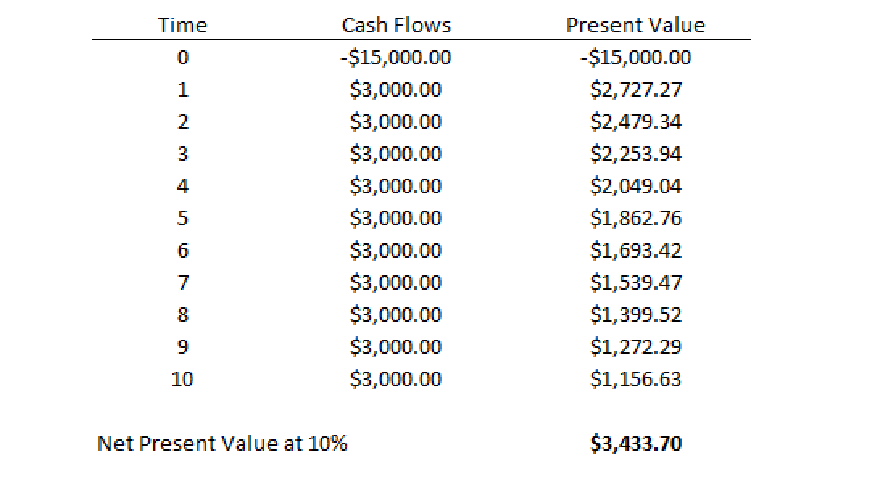
Imagine that you have an opportunity to invest $15,000 to expand your business, and then estimate that this investment will generate $3,000 in profit annually for the next 10 years. Your company's cost of capital, which is used as the discount rate, is 10% per year.
The present value in the table above is the value of each projected cash flow discounted to its equivalent value today. Summing the projected values and subtracting the initial cash outlay of $15,000 produces a net present value for the project of $3,433.70. Since the NPV number is positive, the project is likely to be profitable.
Capital
Advantages and disadvantages of NPV
Advantages and disadvantages of NPV
| NPV Advantages | NPV Disadvantages |
|---|---|
| Incorporates time value of money. | Accuracy depends on quality of inputs. |
| Simple way to determine if a project delivers value. | Not useful for comparing projects of different sizes, as the largest projects typically generate highest returns. |
| Considers a company's cost of capital. | May omit hidden costs such as opportunity costs and organizational costs. |
| Accounts for inherent uncertainty of projections by most heavily discounting far-future estimates. | Purely quantitative in nature and does not consider qualitative factors. |
Related investing topics
Chart by author.
Frequently asked questions about NPV
What is the difference between NPV and IRR?
The internal rate of return (IRR) is the annual rate of return a potential project is expected to generate. IRR is calculated by setting the NPV in the above equation to zero and solving for the rate "r."
While both NPV and IRR can be useful for evaluating a potential project, the two measures are used differently. A project's NPV only needs to be positive for the endeavor to be worthwhile, while the IRR that results from setting the NPV to zero is compared to a company's required rate of return. Projects with IRRs above the required rate of return are generally considered attractive opportunities. IRR is also more useful than NPV for evaluating projects of different sizes.
What is a good NPV?
A positive NPV is a good NPV. A project with a positive NPV should be pursued, while a project with a negative NPV should not. A project with an NPV of zero would confer neither financial benefit nor harm.
However, a "good" NPV is only as good as the inputs into the NPV equation. Simply guessing about a project's future cash flows and the discount rate produces an unreliable NPV that is not very useful.
Why are future cash flows discounted to NPV?
Simply put, because of the time value of money. A dollar in the future is worth less than a dollar today, and incorporating that concept into financial models is the best way to make investment decisions in the present. The future is uncertain, and inflationary pressures further cause the value of a dollar to weaken over time.