If you're interested in assuming more risk to boost your investment returns, then trading options might be worthwhile. Stock options are contracts that give the owner the right -- but not any obligation -- to buy or sell a stock at a certain price by a certain date.
That specified price is known as the strike price, and the standard number of shares an options contract confers the right to buy or sell is 100. The price of the options contract is called its premium, and it is displayed as the price per share. So an options contract with a premium of $1 costs $100 to purchase options on 100 shares.
Using options as part of your investment strategy can be as simple or as complex as you choose, but your first step is to learn more about these derivative securities.
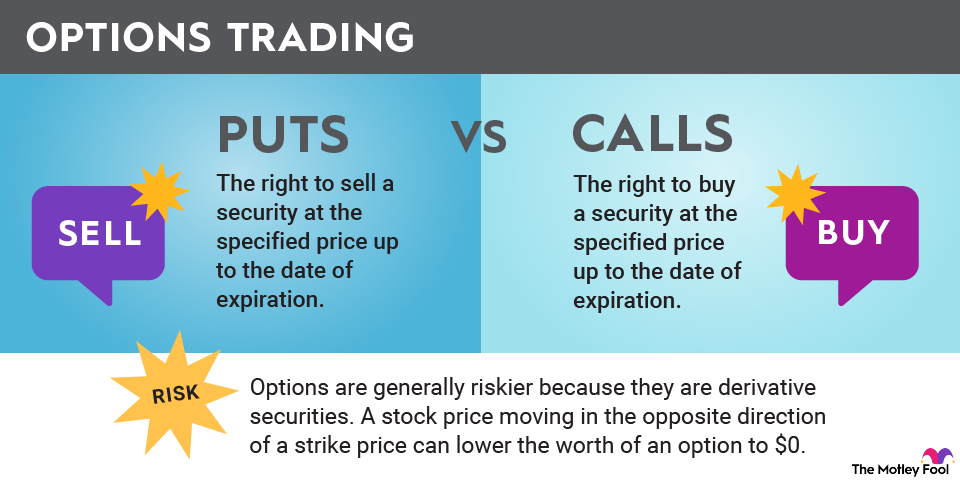
Put versus call options
Options contracts are categorized into two basic types: put options and call options. A put option gives the holder the right to sell a stock at a specific price any time until the option's date of expiration. A call option gives its owner the right to buy a stock at a certain price until the expiration date.
If you buy an options contract, you have control over whether it gets exercised. If you buy a call option, you have the right to buy 100 shares of the specified security. If you buy a put option, you earn the right to sell 100 shares of the stock.
But if you sell an options contract, then you do not control whether the options are exercised. Selling a call option requires you, if the buyer chooses, to sell 100 shares of a stock to the option owner. Selling a put option requires you, if the buyer chooses, to buy 100 shares of a stock from the option owner.
What are the benefits of trading options?
Investors can use options to enhance the performance of their portfolios and gain exposure to individual securities with minimal cash. Buying options is also a way to lower the overall investment risk of a portfolio.
If an investor buys a call option and the stock's price increases to above the strike price before the option's expiration date, then the investor can exercise their option to buy the stock at the strike price and resell it at the higher market price for a profit.
Similarly, if an investor buys a put option and the stock's price decreases to below the strike price before the put option's expiration date, then the investor can exercise their option to sell the stock at the strike price and repurchase it at the lower market price.
Investors can also enhance the performance of their portfolios by selling options. If an investor sells an option and the stock's price does not reach the strike price before the option's expiration date, then the investor's profit equals the premium paid for the options contract.
Using options, you can gain increased exposure to a stock without using a lot of cash. Instead of buying the shares directly, you can buy a call option for a much lower price. As the stock increases in value, the value of the call option also increases, and you have the option of selling that option before its expiration date.
If you already own a stock, then you can use options to decrease the volatility of your investment. Buying a put option can protect you against a crash in a stock's price since you can earn the strike price specified by the contract.
Related investing topics
What are the risks of options trading?
Options are generally riskier because they are derivative securities, meaning they derive their value from another type of security, such as a stock. Options themselves are inherently worthless if decoupled from the underlying asset.
The risk of using options as leverage to boost returns is that using leverage of any sort magnifies portfolio volatility. Also, a stock price moving in the opposite direction of a strike price can lower the worth of an option to $0.
Buying and selling options contracts confers different risks to investors:
Risks of buying options
The risk of buying an option is limited to the price paid for the option itself. If the stock price ends up on the wrong side of an option contracts strike price, it expires worthless.
Risks of selling options
Selling options enables you to collect premiums but can be riskier because the potential for loss can be unlimited. The maximum per-share loss that can be incurred on the sale of a put option is the difference between the strike price and zero (minus the option's premium), while the potential loss on a call option has no maximum since the stock's price can rise to infinity.
Stock option examples
Let's take a look at a real-world options example using Apple (AAPL -3.46%) stock. At the time of this writing, Apple shares trade for $145.70.
Imagine that you expect Apple's share price to climb higher before the end of the year, and that you want to buy a call option.
When purchasing a call option, you have a choice among expiration dates paired with strike prices and premiums. Options can expire within weeks, months, or years.
Since your focus is Apple's share price performance in the latter half of the year, we can focus on options expiring in January of the following year. Here are some of the choices for Apple stock options expiring then:
Option Strike Price | Option Premium |
|---|---|
$130 | $20.50 |
$135 | $17.00 |
$140 | $13.85 |
$145 | $11.20 |
$150 | $8.75 |
$155 | $6.87 |
The options with the lowest strike price are the least risky but also the most expensive. If you buy the options with the $145 strike price, then you'd pay $1,120, which is the premium times 100 shares.
Is options trading right for you?
Options trading is an advanced strategy most often used by sophisticated investors. Buying and selling options profitably requires plenty of research and in-depth understanding of your stock positions. If you don't want to make that type of commitment as an investor, then buy-and-hold investing may be a better approach for you to build wealth.